실험 10. 달의 공전과 위상 변화

Introduction

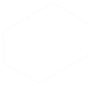
둥근 보름달이 떠오른 날 등산을 하거나 시골길을 걸어본 사람이라면 밤길이 그다지 어둡지 않다는 사실을 알고 있을 것이다. 때로는 밝은 달빛이 만든 그림자에 깜짝 놀라기도 한다. 매일 다른 모습으로 떠오르는 달은 누구에게나 흥미로운 천체다. 음력 한 달을 기준으로 달은 초승달에서 시작해, 상현, 보름, 하현, 그믐까지 모양을 바꾼다. 이러한 변화를 반복하는 이유는 태양과 지구, 달의 상대적인 위치에 따라 태양빛을 반사하는 달 표면이 다른 각도에서 보이기 때문이다.

음력으로 초하루가 지날 쯤이면 해진 후 서쪽 하늘에 가느다란 눈썹 모양의 초승달을 볼 수 있다. 그런데 이 때 “야! 초승달이 떴다!”고 말한다면 이는 잘못된 표현이다. 초승달은 이른 아침에 이미 떠올라 저녁때는 지고 있는 상황이기 때문이다. 온종일 하늘에 떠 있던 초승달이 밝은 태양에 가려 보이지 않았을 뿐이다.

음력 7, 8일이 되면 달은 ‘반달(상현달)’이 되고 밝기도 밝아진다. 물론 달을 볼 수 있는 시간도 자정까지로 길어지게 된다. 음력 15일 경에 볼 수 있는 보름달은 해질 무렵에 동쪽 지평선 위로 떠오를 채비를 서두른다. 반달에 비해 10배가량 밝은 보름달은 밤새 밤하늘을 밝히고 새벽에 이르러서야 서쪽 지평선 너머로 지게 된다.

보름달 이후 크기가 줄어들기 시작한 달은 음력 21일 경에는 다시 ‘반달(하현달)’이 된다. 하현달은 자정 무렵부터 떠오르기 시작한다. 이때부터 달이 뜨는 시간은 점점 새벽으로 가까워지며 음력 29일 경에는 이른 새벽 동쪽에서 그믐달을 볼 수 있다.

음력의 날짜보다 더 정확히 달의 모양을 표현하는 것은 ‘월령’이다. 월령은 말 그대로 달의 나이를 나타내는 것으로 삭(달이 안 보이는 때)을 월령 0일로 해서 달의 모양 변화를 날짜 단위로 나눈 것이다. 삭에서 다음 삭까지는 29.5일이며 월령 14.8일은 보름달을 나타낸다. 음력날짜를 보면 월령을 짐작할 수 있지만 날짜는 실제로 월령보다 1-2일 정도 앞서 간다. 그 이유는 달이 ‘삭’인 날에 월령은 0일이지만 음력에서는 그날을 1일로 삼기 때문이다. 음력과 월령을 알면 달의 뜨고 지는 시각과 밝기, 겉모양 등을 대략 짐작할 수 있다.

이 실험을 통해 주어진 달의 자료를 통해 달의 크기, 지구까지의 거리, 태양-지구-달 사이의 각도를 조사하여 달의 공전 궤도를 그려보자.

Method

[실험 1] 지구에서 달까지의 거리 구하기

⑴ [자료 1] 한 달 동안 달의 위상 변화에서 보이는 달의 크기가 모두 같은가? 같지 않다면 이를 정확하게 측정하기 위해서는 어떤 방법을 사용해야 할까?

⑵ 자신이 생각한 방법으로 달의 크기(지름)와 달의 평균 크기를 구해보자.

⑶ 지구에서 달까지의 평균거리를 384,400km로 생각하고 ⑵에서 구한 달의 크기를 이용하여 지구에서 달까지의 거리를 구해보자.

⑷ 그 결과를 [표 1]에 작성하자.

 

[실험 2] 태양-지구-달 사이의 각도 구하기

⑴ 지구에서 관찰한 태양의 모습과 달리 달은 지구를 공전하면서 그 모양이 바뀌게 된다. 이를 통해 달의 공전궤도상에서의 달의 위치를 정확하게 결정할 수 있다.

# 달의 위상 변화를 대략적으로 나타내보면 다음 그림과 같은 원리에 의한다. # 달의 위상 변화를 기하학적으로 나타내면 다음과 같다.

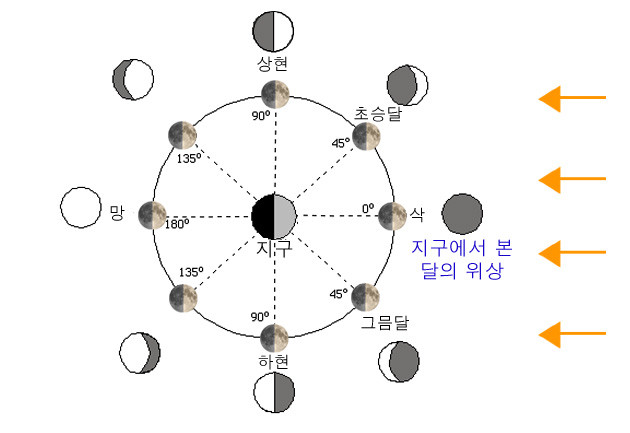
# 이를 이해하기 위해 다음에 나타난 절차대로 생각해 보자. (태양-지구-달이 이루는 각의 크기 : θ, 달의 반지름 : R)   보름달로 보일 때 지구에서 보이는 달의 밝은 부분을 달의 지름과 같은 2R이라고 하면, 앞 그림에서 밝게 보이는 부분 : _____________, 어두워 보이지 않는 부분 : _____________ 이다. 따라서 ,보이는 부분과 어두운 부분의 비는 _____________ 이다.   보름인 경우에 θ=180°이므로 보이는 부분은 2R이 되는 것과 같이, 삭인 경우에 θ= _____________° 이므로, 보이는 부분은 상현 또는 하현인 경우에 θ= _____________°이므로 보이는 부분과 어두운 부분의 비는 _______ : _______ 이다.

⑵ 아래와 같은 방법을 사용하여 태양-지구-달 사이의 각도를 구해보자.

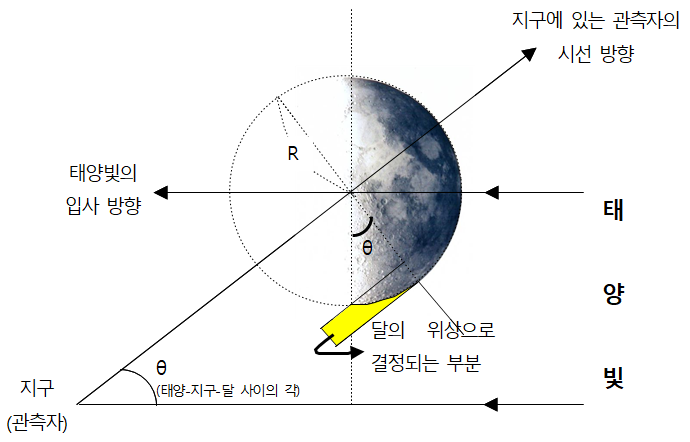
① [실험 1]에서 지구-달 거리를 계산하기 위해 달의 지름을 결정하는 과정을 거쳤다. 이 결과를 활용하여 달의 지름을 긋는다.

② 달 사진에서 보이는 부분(R2)과 어두운 부분(R1)의 길이 비 을 계산하면, 바로 이 값이 _________ 가 되므로 θ를 결정할 수 있다.

⑶ 그 결과를 [표 2]에 작성하자.

 

[실험 3] 달의 궤도 그리기

⑴ [실험 1]에서 계산했던 지구-달 사이의 거리(환산) 자료와 [실험2]에서 구한 태양-지구-달 사이의 각도(θ) 자료를 통해 달의 궤도를 나름대로 정확하게 그려보자.

 

Results

⑴ 자신이 사용한 달의 지름을 정확하게 구하는 방법을 무엇인가?

 

⑵ [실험 1]의 결과

사진 번호	달의 지름(cm)	평균 크기와의 차이	지구 - 달 거리
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

 

⑶ [실험 2]의 결과

사진 번호		θ	사진 번호		θ
1			13
2			14
3			15
4			16
5			17
6			18
7			19
8			20
9			21
10			22
11			23
12

 

⑷ [실험 3]의 결과: 달의 궤도 그리기

 

Discussion (3줄 이내)

 

Assignment

⑴ 신윤복의 ‘월하정인(月下情人)’에서의 달의 위상은 실제로 나타날 수 있는 달의 위상일까? 그렇게 생각한 이유는 무엇인가? 신윤복은 자신의 그림에 왜 이런 달의 위상을 그리게 되었을까?

⑵ [⑴의 문제와 같은 맥락] 아래의 상황을 살펴보고 여러분이 아이디 tmdgus4842인 사람에게 제대로된 설명을 해줘야하는 상황이라면 어떻게 설명을 해 줄 것인지 써보자.

 

 

 

 

Reference