실험 5. 지층의 두께와 지진파의 속도 구하기

1. Introduction

탄성파 탐사법은 크게 굴절법과 반사법으로 나눌 수 있다. 굴절법은 탄성파의 전파과정에서 임계굴절이 일어날 경우에만 사용할 수 있다. 즉, 속도가 낮은 상부층에서 속도가 높은 하부층에 임계각으로 입사한 파는 층의 경계면에 평행하게 굴절된다. 이 때 에너지는 경계면을 따라 하부층의 속도로 전파하며, 에너지의 일부는 연속적으로 상층부로 재굴절하여 지표에 도달하게 된다. 탄성파 굴절법을 이용하여 지층의 탄성과 전달속도와 두께를 구하는 원리와 방법을 익혀 그 응용에 관하여 학습해보자.

2. Background

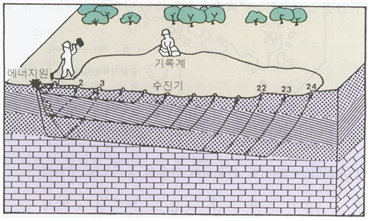
지표 부근의 암층에 대한 탄성파 전달속도 분포와 그 두께에 관한 정보는 대형 건축물의 건설이나 도로나 교량건설 등의 토목공사에 있어서 매우 중요한 설계 자료이다. 이들 지표 부근에 대한 조사는 주로 탄성파의 굴절 원리를 이용한 탄성파 탐사법으로 이루어진다. 탄성파 탐사법은 지표면에 수진기(geophone)를 설치한 후, 해머 또는 폭발물에 의하여 인공지진을 일으켜 발생한 지진파가 도달하는 시간을 측정하여 조사하는 방법이다[그림 1].

그림 1 탄성파 탐사 모식도

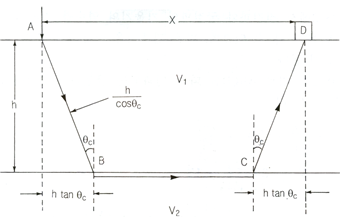
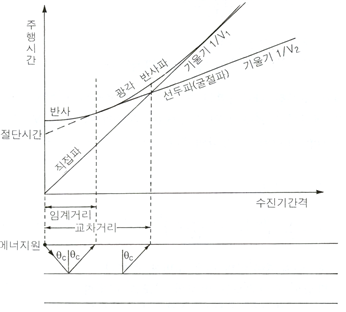
지하의 암층경계면에 입사한 탄성파는 반사(reflection) 또는 굴절(refraction)을 일으키며 전파되는데, 이 중에서 임계각으로 입사한 파는 90°의 굴절을 일으켜 경계면 하부층의 속도로 전파되어, 상부층으로 전달되는 직접파보다 빨리 수진기에 도착하게 된다. 이러한 파를 선두파(head wave)라 하며, 탄성파 굴절법은 이들 선두파의 신호를 분석하여 지층의 속도와 두께를 알아내는 방법이다. 탄성파 전달속도가 각각 V₁과 V₂(V₂>V₁)인 수평구조를 가정하면(그림 2), 음원에서 나오는 탄성파는 직접파, 반사파 및 굴절파로 전달되어 각 수진기에 기록되는데, 거리에 따른 도달시간을 나타내면 [그림 3]과 같으며, 이 도표를 주시곡선(T-X Diagram)이라 한다.

그림 2 수평 2층 구조에서의 굴절파 경로

그림 3 탄성파 탐사 자료의 주시곡선도

[그림 3]에서 직접파와 굴절파의 기울기의 역수를 취하면 각 층의 속도 V₁과 V₂를 구할 수 있으며, 다음 관계식을 이용하여 층의 두께(h)도 구해낼 수 있게 된다.

(1) 직접파의 도달 시간(T_d)

[그림 2]의 경로 AD를 따라 전파되는 직접파가 D점까지 도달하는데 걸리는 시간 T_d는

$$T_d = {{X} \over {V_1}} $$

이다.

(2) 굴절파의 도달 시간( )

[그림 2]의 경로 ABCD를 따라 전파되는 굴절파가 D점까지 도달하는데 걸리는 시간 $$T_r$$은

$$T_r = { AB \over V_1 } + {BC \over V_2} + {CD \over V_1}$$

$$ = {1 \over V_1}{h \over \cos \theta _c }+ { X-2h \tan \theta _c \over V_2 } + { 1 \over V_1}{h \over \cos \theta _c }$$

$$ = {2 \over V_1} {h \over \cos \theta _c } + {X \over V_2 }-{2h \tan \theta _c \over V_2}$$

$$= 2h \left ( {1 \over V_1 \cos \theta _c } - {\tan \theta _c \over V_2} \right ) + {X \over V_2}$$

$$= 2h \left ( {1 \over V_1 \cos \theta _c } - { 1 \over V_2} {\sin theta _c \over \cos \theta _c } \right ) + {X \over V_2}$$

$$ = 2h \left ( {1 \over V_1 \cos \theta _c } - { 1 \over V_2} {\sin \theta _c \over \cos \theta _c } \right ) + {X \over V_2}$$

$$= {2h \over {V_1 \cos \theta _c}} \left ( 1 - {{V_1}\over {V_2}} \sin \theta _c \right) + {{X} \over {V_2}}$$

가 임계각이라는 점을 감안하여 스넬의 법칙을 이용하면,

$$ {V_1 \over V_2} = \sin \theta _c $$

이므로,

$$T_r = { 2h \over {V_1 \cos \theta _c} } (1- \sin ^2 \theta _c )+ {X \over V_2}$$

$$={2h \over V_1 \cos \theta _c} (\cos ^2 \theta _c)+ {X\over V_2}$$

$$= {2h \cos \theta _c \over V_1 } + {X \over V_2} $$

이 된다. 즉, 굴절파의 주시곡선은 를 기울기로 하고, 을 y절편으로 하는 직선이 된다.

한편,

이므로,

가 된다.

교차거리( )에서는 직접파의 도달시간( )과 굴절파의 도달시간이 같으므로

이 성립한다.

한편, 탄성파 전달속도는 암석의 밀도를 비롯한 물리적 특성에 따라 달라진다. 물리적 특성은 암성의 구성광물, 공극률, 함수량, 변성정도 등에 의하여 지배되며, 각종 암석의 탄성파 전달속도는 [표 1]과 같다.

암 석	속 도( )	암 석	속 도( )
풍화암	305~610	셰일	2750~4270
자갈, 모래(건)	468~915	백악	1830~3970
모래(습)	610~1830	석회암	2140~6100
점토	915~2750	암염	4270~5190
물	1430~1680	화강암	4580~5800
해수	1460~1530	변성암	3050~7020
사암	1830~3970	얼음	3673

3. Method & Result

[그림 4]는 지진파 기록계를 이용하여 얻은 탄성파 탐사 자료이다. 이용된 장비는 다중채널(multichannel) 탄성파 기록계로써 한 탄성파원(source)으로부터 24개의 수신기에 기록된 탄성파 기록이다. 파형의 흑색부분이 양(+)의 진폭을 나타낸다. 각 수진기간의 거리는 4m이다.

[그림 4]의 탄성파 기록을 [그림 3]과 비교하여 직접파, 굴절파를 서로 다른 색으로 구별한다.

4. Discussion

⑴ 직접파와 굴절파의 주시곡선 기울기로부터 각 층의 속도를 구하여라.

⑵ 주시곡선으로부터 교차거리 를 구하여라.

⑶ 상부층의 두께를 계산하여라.

⑷ 상부층의 속도와 두께로 볼 때, 이 층의 구성은 어떠한 층이라고 생각하는가?